[ Home ] [ Up ] [ 1: CIA Hiring ] [ 2: Brobdingnag Battles ] [ 3: Delta Force ] [ 4: Ethnic Dispute ] [ 5: CIA Hiring (continued) ]

Refer to the CIA Hiring problem seen earlier.

You determined how many ways there were of selecting 2 applicants from a total of 5, by simply enumerating all the possibilities.

There is a specific probability term for this (the number of ways of arranging k objects from a set of n objects without regard to the order in which the objects are arranged).

Think:

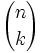
1. Determine the above term, and use the corresponding associated formula to calculate the number (call it N) you determined by simple enumeration.  Verify that the two results agree.
   
2. Consider an event, A, where exactly one of the two best applicants appears in a selection of 2 out of 5 applicants.  

   The CIA would like to find out the number of ways that this can happen (i.e. the number of sample points) n_A, and also the probability of this event happening, P(A). 

   Your mission (should you choose to accept it ) is to answer the CIA's questions.

Here are the steps to accomplish this:

1. Determine the number of ways of selecting one of the 2 best applicants, m. 

   Determine the number of ways of selecting one of the 3 least competent applicants, n.

2. Determine n_A by multiplying the above two results.  Explain why this works.

   You can verify that this value is correct by going back to your enumeration of pairs in the original problem, and counting how many pairs contain exactly one of the two best applicants.

3. Assuming, as before, that every selection is equally probable, and using the value for n_A you have just determined, calculate the probability of A occurring.